8 31 постоянная больцмана единицы измерения. Людвиг Больцман: Именные достижения

Постоя́нная Бо́льцмана ( k {\displaystyle k} или k B {\displaystyle k_{\rm {B}}} ) - физическая постоянная , определяющая связь между температурой и энергией . Названа в честь австрийского физика Людвига Больцмана , сделавшего большой вклад в статистическую физику , в которой эта постоянная играет ключевую роль. Её значение в Международной системе единиц СИ согласно изменения определений основных единиц СИ (2018) точно равно

Связь между температурой и энергией

В однородном идеальном газе , находящемся при абсолютной температуре T {\displaystyle T} , энергия, приходящаяся на каждую поступательную степень свободы , равна, как следует из распределения Максвелла , k T / 2 {\displaystyle kT/2} . При комнатной температуре (300 ) эта энергия составляет 2 , 07 × 10 − 21 {\displaystyle 2{,}07\times 10^{-21}} Дж , или 0,013 эВ . В одноатомном идеальном газе каждый атом обладает тремя степенями свободы, соответствующими трём пространственным осям, что означает, что на каждый атом приходится энергия в 3 2 k T {\displaystyle {\frac {3}{2}}kT} .

Зная тепловую энергию, можно вычислить среднеквадратичную скорость атомов, которая обратно пропорциональна квадратному корню атомной массы. Среднеквадратичная скорость при комнатной температуре изменяется от 1370 м/с для гелия до 240 м/с для ксенона . В случае молекулярного газа ситуация усложняется, например, двухатомный газ имеет 5 степеней свободы - 3 поступательных и 2 вращательных (при низких температурах, когда не возбуждены колебания атомов в молекуле и не добавляются дополнительные степени свободы).

Определение энтропии

Энтропия термодинамической системы определяется как натуральный логарифм от числа различных микросостояний Z {\displaystyle Z} , соответствующих данному макроскопическому состоянию (например, состоянию с заданной полной энергией).

Коэффициент пропорциональности k {\displaystyle k} и есть постоянная Больцмана. Это выражение, определяющее связь между микроскопическими ( Z {\displaystyle Z} ) и макроскопическими состояниями ( S {\displaystyle S} ), выражает центральную идею статистической механики.

Постоя́нная Бо́льцмана ( k {\displaystyle k} или k B {\displaystyle k_{\rm {B}}} ) - физическая постоянная , определяющая связь между температурой и энергией . Названа в честь австрийского физика Людвига Больцмана , сделавшего большой вклад в статистическую физику , в которой эта постоянная играет ключевую роль. Её значение в Международной системе единиц СИ согласно изменения определений основных единиц СИ (2018) точно равно

Связь между температурой и энергией

В однородном идеальном газе , находящемся при абсолютной температуре T {\displaystyle T} , энергия, приходящаяся на каждую поступательную степень свободы , равна, как следует из распределения Максвелла , k T / 2 {\displaystyle kT/2} . При комнатной температуре (300 ) эта энергия составляет 2 , 07 × 10 − 21 {\displaystyle 2{,}07\times 10^{-21}} Дж , или 0,013 эВ . В одноатомном идеальном газе каждый атом обладает тремя степенями свободы, соответствующими трём пространственным осям, что означает, что на каждый атом приходится энергия в 3 2 k T {\displaystyle {\frac {3}{2}}kT} .

Зная тепловую энергию, можно вычислить среднеквадратичную скорость атомов, которая обратно пропорциональна квадратному корню атомной массы. Среднеквадратичная скорость при комнатной температуре изменяется от 1370 м/с для гелия до 240 м/с для ксенона . В случае молекулярного газа ситуация усложняется, например, двухатомный газ имеет 5 степеней свободы - 3 поступательных и 2 вращательных (при низких температурах, когда не возбуждены колебания атомов в молекуле и не добавляются дополнительные степени свободы).

Определение энтропии

Энтропия термодинамической системы определяется как натуральный логарифм от числа различных микросостояний Z {\displaystyle Z} , соответствующих данному макроскопическому состоянию (например, состоянию с заданной полной энергией).

Коэффициент пропорциональности k {\displaystyle k} и есть постоянная Больцмана. Это выражение, определяющее связь между микроскопическими ( Z {\displaystyle Z} ) и макроскопическими состояниями ( S {\displaystyle S} ), выражает центральную идею статистической механики.

Согласно закону Стефана – Больцмана плотность интегрального полусферического излучения E 0 зависит только от температуры и изменяется пропорционально четвертой степени абсолютной температуры T :

Стефана – Больцмана постоянная σ 0 – физическая постоянная, входящая в закон, определяющий объемную плотность равновесного теплового излучения абсолютно черного тела:

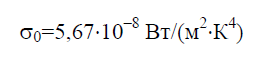
Исторически закон Стефана-Больцмана был сформулирован раньше закона излучения Планка, из которого он вытекает как следствие. Закон Планка устанавливает зависимость спектральной плотности потока излучения E 0 от длины волны λ и температуры T :

где λ – длина волны, м; с =2,998 10 8 м/с – скорость света в вакууме; Т – температура тела, К;
h = 6,625 ×10 -34 Дж×с– постоянная Планка.

Физическая постоянная k , равная отношению универсальной газовой постоянной R =8314Дж/(кг× K) к числу Авогадро NA =6,022× 10 26 1/(кг× моль):

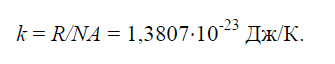
Число различных конфигураций системы из N частиц для данного набора чисел n i (число частиц, находящихся в i -том состоянии, которому соответствует энергия e i ) пропорционально величине:

Величина W есть число способов распределения N частиц по энергетическим уровням. Если справедливо соотношение (6) то считается, что исходная система подчиняется статистике Больцмана. Набор чисел n i , при котором число W максимально, встречается наиболее часто и соответствует наиболее вероятному распределению.

Физическая кинетика – микроскопическая теория процессов в статистически неравновесных системах.

Описание большого числа частиц может успешно осуществляться вероятностными методами. Для одноатомного газа состояние совокупности молекул определяется их координатами и значениями проекций скоростей на соответствующие координатные оси. Математически это описывается функцией распределения, характеризующей вероятность пребывания частицы в данном состоянии:

есть ожидаемое число молекул в объеме d d , координаты которых находятся в интервале от до +d , а скорости в интервале от до +d.

Если осредненной по времени потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией, то газ называется идеальным. Идеальный газ называется газом Больцмана, если отношение длины пробега молекул в этом газе к характерному размеру течения L конечно, т.е.

т.к. длина пробега обратно пропорциональна nd 2 (n – числовая плотность 1/м 3 , d – диаметр молекулы, м).

Величину

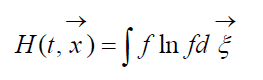
называют H -функцией Больцмана для единицы объема, которая связана с вероятностью обнаружения системы из молекул газа в данном состоянии. Каждому состоянию соответствуют определенные числа заполнения шестимерных пространственно-скоростных ячеек, на которые может быть разбито фазовое пространство рассматриваемых молекул. Обозначим W вероятность того, что в первой ячейке рассматриваемого пространства окажется N 1 молекул, во второй N 2 и т.д.

С точностью до постоянной, определяющей начало отсчета вероятности, правомерно соотношение:

,

где 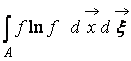– H-функция области пространства А , занятой газом. Из (9) видно, что W и H взаимосвязаны, т.е. изменение вероятности состояния приводит к соответствующей эволюции H функции.

Больцмана принцип устанавливает связь между энтропией S физической системы и термодинамической вероятностью W её состояния:

(печатается по изданию: Коган М.Н. Динамика разреженного газа. – М.: Наука, 1967.)

Общий вид КУБ:

где – массовая сила, обусловленная наличием различных полей (гравитационного, электрического, магнитного), действующая на молекулу; J – интеграл столкновений. Именно этот член уравнения Больцмана учитывает столкновения молекул друг с другом и соответствующие изменения скоростей взаимодействующих частиц. Интеграл столкновений представляет собой пятимерный интеграл и имеет следующую структуру:

Уравнение (12) с интегралом (13) получено для столкновения молекул, при которых не возникает тангенциальных сил, т.е. сталкивающиеся частицы считаются идеально гладкими.

В процессе взаимодействия внутренняя энергия молекул не меняется, т.е. предполагается, что эти молекулы являются идеально упругими. Рассматриваются две группы молекул, имеющих до соударения друг с другом (столкновения) скорости и (рис. 1), а после столкновения соответственно скорости и . Разность скоростей и называется относительной скоростью, т.е. . Ясно, что для гладкого упругого столкновения . Функции распределения f 1 ", f", f 1 ,f описывают молекулы соответствующих групп после и до столкновений, т.е. ; ; ; .

Рис. 1. Столкновение двух молекул.

В (13) входят два параметра, характеризующие расположение сталкивающихся молекул друг относительно друга: b и ε; b – прицельное расстояние, т.е. наименьшее расстояние, на которое сблизились бы молекулы при отсутствии взаимодействия (рис. 2); ε называют угловым параметром столкновений (рис. 3). Интегрирование по b от 0 до ¥ и по от 0 до 2p (два внешних интеграла в (12)) охватывает всю плоскость силового взаимодействия перпендикулярно вектору

Рис. 2. Траектория движения молекул.

Рис. 3. Рассмотрение взаимодействия молекул в цилиндрической системе координат: z , b , ε

Кинетическое уравнение Больцмана выведено при следующих допущениях и предположениях.

1. Считается, что происходит в основном столкновения двух молекул, т.е. роль столкновений одновременно трех и большего числа молекул незначительна. Это допущение позволяет использовать для анализа одночастичную функцию распределения, которая выше названа просто функцией распределения. Учет столкновения трех молекул приводит к необходимости использования в исследовании двухчастичной функции распределения. Соответственно анализ существенно усложняется.

2. Предположение о молекулярном хаосе. Оно выражается в том, что вероятности обнаружения частицы 1 в фазовой точке и частицы 2 в фазовой точке независимы друг от друга.

3. Равновероятны столкновения молекул с любым прицельным расстоянием, т.е. функция распределения не меняется на диаметре взаимодействия. Необходимо отметить, что анализируемый элемент должен быть малым, чтобы f в пределах этого элемента не менялась, но в то же время чтобы не была велика относительная флуктуация ~ . Потенциалы взаимодействия, используемые при вычислении интеграла столкновений, являются сферически симметричными, т.е. .

Распределение Максвелла-Больцмана

Равновесное состояние газа описывается абсолютным Максвелловским распределением, которое является точным решением кинетического уравнения Больцмана:

где m – масса молекулы, кг.

Общее локально-максвелловское распределение иначе называемое распределение Максвелла-Больцмана:

в том случае, когда газ движется как целое со скоростью и переменные n , T зависят от координаты
и времени t .

В поле тяготения Земли точное решение уравнения Больцмана показывает:

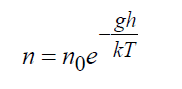
где n 0 = плотность у поверхности Земли, 1/м 3 ; g – ускорение силы тяжести, м/с 2 ; h – высота, м. Формула (16) является точным решением кинетического уравнения Больцман либо в безграничном пространстве, либо при наличии границ, не нарушающих этого распределения, при этом температура также должна оставаться постоянной.

Эта страница оформлена Пузиной Ю.Ю. при поддержке Российского Фонда Фундаментальных Исследований – проект №08-08-00638.

Главная » Понятие » 8 31 постоянная больцмана единицы измерения. Людвиг Больцман: Именные достижения